Я ☞ Tutorials ☞ Trapping rain water - 1

Imagine we have walls of different hights. After raining we will get some gaps filled with water. We need to compute the volume of water accumulated in gaps between these walls:

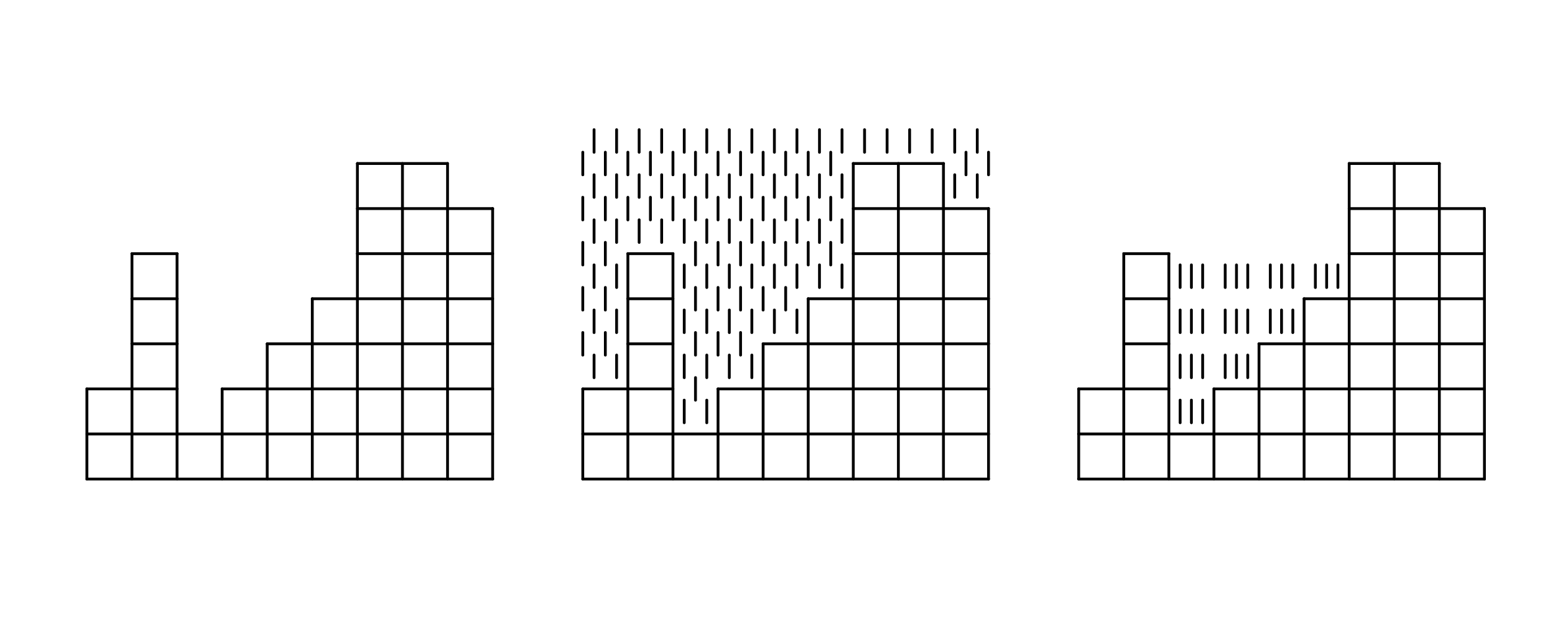
We take a lowest of left and right peak heights, subtract minimal peak height from the current wall’s height and voila - we have a volume of trapped water:

trap left right level = min left right - level

To compute a peak for each wall level we need to traverse a list. However, computing left and right peaks are opposite to each other. Computing left peak could be performed forwards since we already know the previous highest peak. So with the right peak we should traverse a list of wall levels backwards.

wall = 2, 5, 1, 2, 3, 4, 7, 7, 6
 
wall `yokl` Forth `ha` State `ha` Event `ha_` max `ho'ho` auto `AR_` 2, 5, 5, 5, 5, 5, 7, 7, 7
wall `yokl` Prior `ha` State `ha` Event `ha_` max `ho'ho` auto `AR_` 7, 7, 7, 7, 7, 7, 7, 7, 6

As soon as we have wall levels with left and right peaks we are ready to compute trapped water in each gap. We need to adjust our trap expression application since we have a tuple of three values (left peak, right peak and a wall level) and an accumulator - we do everything statefully.

gap = (trap `hj'hj`) where

trap left right origin all = min left right - origin + all

This time, it doesn’t really matter how we traverse a structure - forwards or backwards, since + is assosiative.

odds `yokl` Prior `ha` State `ha` Event `ha_` gap `ho'ho` auto `AR_` 0, 4, 7, 9, 10, 10, 10, 10, 10

This is how we can put it all together:

tap = is `ho'yokl` (gap `ho'ho` auto `ho` Event `ho` State `ho` New `ho` Forth) `ho'he'he'hv` 0 `ho` this
 `ha__` is `ho'yokl` (max `ho'ho` auto `ho` Event `ho` State `ho` New `ho` Forth) `ho'he'he'hv` 0 `ho` this
 `lo'yp` is `ho'yokl` (max `ho'ho` auto `ho` Event `ho` State `ho` New `ho` Prior) `ho'he'he'hv` 0 `ho` this
 `lo'yp` is @(Nonempty List Integer)

main = tap `ha` Nonempty @List
 `ha` Item 2 `ha` Maybe `ha` Next
 `ha` Item 5 `ha` Maybe `ha` Next
 `ha` Item 1 `ha` Maybe `ha` Next
 `ha` Item 2 `ha` Maybe `ha` Next
 `ha` Item 3 `ha` Maybe `ha` Next
 `ha` Item 4 `ha` Maybe `ha` Next
 `ha` Item 7 `ha` Maybe `ha` Next
 `ha` Item 7 `ha` Maybe `ha` Next
 `ha` Item 6 `ha` Maybe `hv` Last
 `yokl_` Forth `ha` Run `ha` print

So with the levels were shown at the top, we should get trapped water volume 10.

Full source code is available here.